leetcode 算法题解法
排序部分
排序算法总结
算法分类
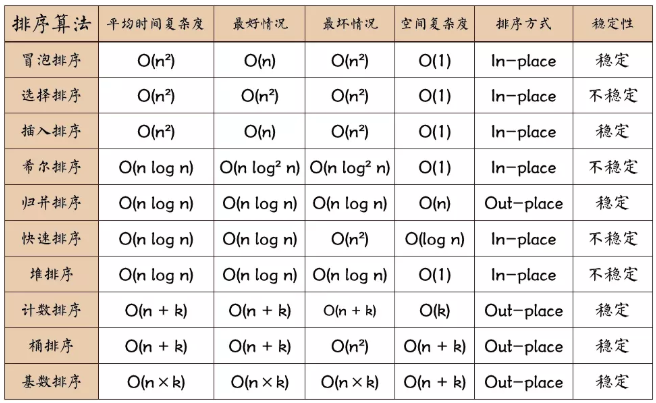
冒泡排序
- 稳定
- 对相邻的元素进行两两比较,顺序相反则进行交换,这样,每一趟会将最小或最大的元素“浮”到顶端,最终达到完全有序。就好像一串气泡一样,最终从小到大或从大到小依次排下来。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15vector<int> bubble(vector<int> nums) {
// 第一层循环从最后一个数字开始
// 每经历一次最外层循环,i位上的数确定下来
for (int i = nums.size()-1; i > 0; --i) {
// 用于从0开始依次冒泡,将较大的数往后推
for (int j = 0; j < i; ++j){
if (nums[j] > nums[j+1]) {
int temp = nums[j+1];
nums[j+1] = nums[j];
nums[j] = temp;
}
}
}
return nums;
}
选择排序
- 不稳定
- 每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
- 比如序列[5, 5, 3]第一次就将第一个[5]与[3]交换,导致第一个5挪动到第二个5后面
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15vector<int> choose(vector<int> nums) {
// 第一层循环从第一个数字开始
// 每经历一次最外层循环,i位上的数确定下来
for (int i = 0; i < nums.size()-1; ++i) {
// 依次将nums[i]和后面的数进行比较,将最小的数放到i位
for (int j = i+1; j < nums.size(); ++j){
if (nums[j] < nums[i]) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
}
return nums;
}
插入排序
- 稳定
- 把一个新的元素插入已排好序的数组形成一个新的已排好序的数组 从第一个元素开始,取下一个元素比较后实现排序,形成新的数组, 再取第三个元素与该数组比较, 比较时从该数组的最后一位开始比较, 若新元素比与其比较的元素小,则将该比较的元素后移以为, 直到新元素比该数组左边找到其应该插入的位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20vector<int> insert(vector<int> nums) {
// 插入排序默认从第二个数开始
for (int i = 1; i < nums.size(); ++i) {
// 记录下这个值
int temp = nums[i];
// 开始值前一个位置
int j = i-1;
while (j >= 0) {
// 找到被排序数的位置
if (temp >= nums[j]) {
break;
}
// 被排序位置比nums[j]小,将nums[j]往后移动,继续和前面的比较
nums[j+1] = nums[j];
j--;
}
nums[j+1] = temp;
}
return nums;
}
快速排序
- 思路详情请见连接
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41class Solution {
public:
vector<int> quickSort(vector<int>& nums) {
quick(nums, 0, nums.size()-1);
return nums;
}
private:
void quick(vector<int>& nums, int originLeft, int originRight) {
if (originLeft > originRight) {
return;
}
int left = originLeft, right = originRight, baseValue = nums[originLeft];
while (left < right) {
// 移动右边 (划重点,一定要先移动右边的啊!!!)
while (left < right && nums[right] >= baseValue) {
right--;
}
// 移动左边
while (left < right && nums[left] <= baseValue) {
left++;
}
if (left < right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
}
// 调换base
nums[originLeft] = nums[left];
nums[left] = baseValue;
// 递归
quick(nums, originLeft, left-1);
quick(nums, left+1, originRight);
}
};
归并排序
归并排序具体工作原理如下(假设序列共有n个元素):
- 将序列中每相邻的两个数字进行归并操作(merge), 形成 floor(n/2)个序列排序之后每个序列包含两个元素
- 将上述序列在此进行归并,形成 floor(n/4)个序列,每个序列包含四个元素
- 重复步骤二,知道所有的元素排序完毕
归并排序是稳定的排序算法,时间复杂度为O(nlogn),如果是使用链表实现的话,空间复杂度可以达到O(1)
但是如果是使用数组来存储的话,在归并的过程中,需要临时的空间来储存归并好的数据,所以空间复杂度为O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58class Solution {
public:
bool mergeSort(vector<int>& nums) {
int base = 1, size = nums.size();
while (base < size) {
for (int i = 0; i < size; i = i + base*2) {
merge(nums, i, i+base, i + base*2);
}
base = base * 2;
}
}
private:
// for example
// startIndex = 0
// middleIndex = 4
// endIndex = 8
void merge(vector<int>& nums, int startIndex, int middleIndex, int endIndex) {
int size = nums.size();
if (middleIndex >= size) {
middleIndex = size;
endIndex = size;
} else if (endIndex >= size) {
endIndex = size;
}
int i = startIndex, j = middleIndex;
vector<int> temp;
while (i < middleIndex && j < endIndex) {
if (nums[j] < nums[i]) {
temp.push_back(nums[j]);
j++;
} else {
temp.push_back(nums[i]);
i++;
}
}
if (i == middleIndex) {
while (j < endIndex) {
temp.push_back(nums[j]);
j++;
}
} else {
while (i < middleIndex) {
temp.push_back(nums[i]);
i++;
}
}
for (int i = 0; i < temp.size(); ++i) {
nums[startIndex+i] = temp[i];
}
}
};
堆排序
1 |
|