堆

• 堆的一个经典的实现是完全二叉树(complete binary tree)。这样实现的堆成为二叉堆(binary heap)。

• 完全二叉树是增加了限定条件的二叉树。假设一个二叉树的深度为n。为了满足完全二叉树的要求，该二叉树的前n-1层必须填满，第n层也必须按照从左到右的顺序被填满，比如下图:

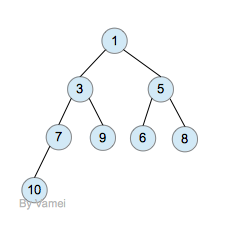
• 为了实现堆的操作，我们额外增加一个要求: 任意节点的优先级不小于它的子节点。如果在上图中，设定小的元素值享有高的优先级，那么上图就符合该要求。

• 这类似于“叠罗汉”。叠罗汉最重要的一点，就是让体重大的参与者站在最下面，让体重小的参与者站在上面 (体重小，优先级高)。为了让“堆”稳固，我们每次只允许最上面的参与者退出堆。也就是，每次取出的优先级最高的元素。

• 堆的主要操作是插入和删除最小元素(元素值本身为优先级键值，小元素享有高优先级)。在插入或者删除操作之后，我们必须保持该实现应有的性质:

  1. 完全二叉树
  2. 每个节点值都小于或等于它的子节点。

插入

• 在插入操作的时候，会破坏上述堆的性质，所以需要进行名为percolate_up的操作，以进行恢复。新插入的节点new放在完全二叉树最后的位置，再和父节点比较。如果new节点比父节点小，那么交换两者。交换之后，继续和新的父节点比较…… 直到new节点不比父节点小，或者new节点成为根节点。这样得到的树，就恢复了堆的性质。

• 我们插入节点2:

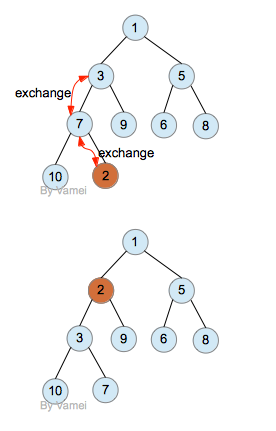
删除

• 删除操作只能删除根节点。根节点删除后，我们会有两个子树，我们需要基于它们重构堆。进行percolate_down的操作: 让最后一个节点last成为新的节点，从而构成一个新的二叉树。再将last节点不断的和子节点比较。如果last节点比两个子节点中小的那一个大，则和该子节点交换。直到last节点不大于任一子节点都小，或者last节点成为叶节点。

• 删除根节点1。如图:

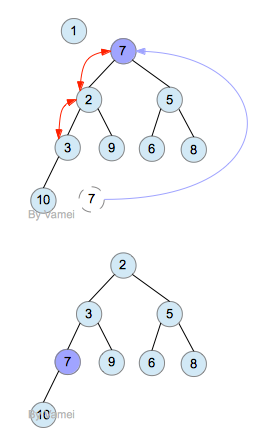
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

func HeapSort(s []int) {
	N := len(s) - 1 // 默认是从这个数组的 index = 1 的位置开始进行堆的构造
	for k := N / 2; k >= 1; k-- {
		sink(s, k, N)
    }
    // 到上面一步位置，已经构造好了一个最大堆，堆顶元素是最大的

    // 下面开始进行排序
	for N > 1 {
		swap(s, 1, N) // 将最大的放到最后一位
		N-- // 减少堆的大小，即最大的元素不动了
		sink(s, 1, N) // 重新构造堆，使得最大元素到堆顶
	}
}

func sink(src []int, k, N int) {
	for {
		i := k * 2
		if i > N {
			break
		}

		if i < N && src[i+1] > src[i] {
			i++
		}

		if src[i] <= src[k] {
			break
		}

		// swap
		swap(src, i, k)
		k = i
	}
}

func swap(s []int, i, j int) { s[i], s[j] = s[j], s[i] }

算法题

计算一个无序数组的中位数

普通的算法

• 先进行排序，然后再计算中位数

使用堆

• 奇数个为例
• 先拿出 (N/2 + 1) 个元素出来构造一个最大堆，拿剩余的元素一个一个比，如果大于堆顶，直接丢弃
• 如果小于堆顶，替换堆顶，重新生成一次堆
• 直到最后一个数

o(1) 时间复杂度获取一个栈的最小元素

• 在维护数据栈之外，维护另外一个栈（排序栈），每次push的时候，将其压入数据栈中
• 将排序栈的栈顶元素于待压入的元素比较大小，压入较小的那一个
• 每次 pop 的时候两个栈同时 pop，这样就可以保持 o(1)复杂度获取最小元素